|
Inhoudsopgave
1.
1.1.
2.
2.1.
2.2.
2.3.
2.4.
3.
3.1.
3.2.
4.
4.1.
4.2.
4.3.
5.
5.1.
5.2.
5.3.
6.
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
7.
8.
8.1.
8.2.
8.2.1.
8.2.2.
8.2.3.
8.3.
9.
9.1.
9.2.
9.3.
9.4.
9.4.1.
9.4.2.
9.4.3.
9.4.4.
9.5.
1.
Deze lessen zijn gemaakt omdat ik vond dat er behoefte aan was bij ons op het werk ( M. de Koning b.v. zie http://www.mdekoning.nl ). De reden dat ik het publiceer is zodat iedereen die er wat aan heeft het kan gebruiken. Dit is allemaal eigen en origineel werk. Alles wat je wil of kan gebruiken mag je gebruiken in wat voor vorm dan ook. Op mijn web site http://ton.vangessel.cl/werk. Zal ik in de toekomst ook de ( texmacs ) bronnen plaatsen en de losse ( xfig en EPS ) plaatjes. Die mag je naar eigen inzicht gebruiken en/of wijzigen. Ik zou me vereerd voelen als je ergens mijn naam vermeld maar het is niet echt nodig.
1.1.
Ik wil graag een aantal mensen in het bijzonder bedanken
Ten eerste de kunstenaar Sija Vermaat van wie ik de computer heb gekregen waarop ik dit maak. ( zie http://www.kunstkringvoorne.nl/vermaat_sija.htm )
Ten tweede Tasman Webdesign van wie ik de server ruimte heb gekregen waar mijn website op draait en die ook de domijnnaam registratie heeft verzorgd (zie http://www.tasman-webdesign.com )
Mijn werk waar ik het beeldscherm van heb waar ik dit op maak (zie http://www.mdekoning.nl)
Mijn vriendin Dymphie Embrechts ( die me al die uren heet moeten missen )
En alle mensen die vroeger de moeite hebben genomen om me dingen wel goed uit te leggen.
2.
2.1.
Alvorens we over stroom spanning en weerstand gaan praten vind ik het eerst van belang om eerst even kort uit te leggen wat nu eigenlijk elektriciteit precies is. Ik ga er niet al te diep op in want je hebt het op school ook al eens gehad.
Aan de basis van de elektro ligt het atoom. Een atoom is opgebouwd uit een kern met daarin positief geladen protonen en ongeladen neutronen. Om die kern heen draaien de negatief geladen elektronen. Het aantal protonen en het aantal elektronen is gelijk aan elkaar. De positieve en de negatieve ladingen houden elkaar in evenwicht. Het aantal elektronen en dus ook het aantal protonen zegt wat voor materiaal het is. In afbeelding 1 zie je een atoom met 2 protonen en twee elektronen. (helium).
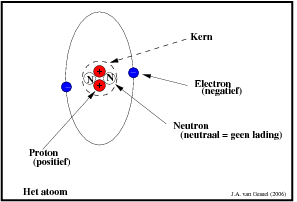 |
Bij electro zijn alleen de electronen van belang. Zoals gezegd houden het aantal protonen en electronen elkaar in evenwicht. Wat gebeurt er nu als je bij een atoom er een electron bij wilt duwen? Dan krijg je een situatie als bij figuur 2. De nieuwe electron duwt de oude weg en die duwt weer de volgende weg. Er ontstaat een stroom van electronen ( ja inderdaad stroom ).
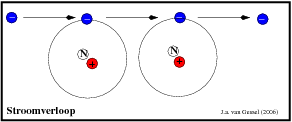 |
Als je een elektron ergens bij wil duwen moet je dus een elektron over hebben. Als je extra elektronen hebt is de kant waar je extra elektronen hebt negatief geladen. Want een elektron is negatief geladen .Dus loopt stroom van min naar plus. Je zal misschien denken die is gek stroom loopt van plus naar min. De reden dat we leren dat stroom van plus naar min loopt is omdat stroom veel eerder is ontdekt dan atomen. Toen de atomen werden ontdekt waren er al zoveel toepassingen gebaseerd op het principe dat stroom van plus naar min loopt dat we het maar zo hebben gelaten. Voor de meeste situaties maakt het ook niet uit. De enigste keer dat je het misschien zal merken is als ze je de werking van half-geleiders uitleggen.
2.2.
Stroom is , zoals je hier boven al hebt kunnen zien , de verplaatsing van elektronen. Je zou kunnen zeggen xxx elektronen per seconde is 1 ampère.
Er kan alleen maar stroom vloeien als er sprake is van een gesloten stroomkring. Dat wil zeggen dat er alleen een stroom kan vloeien als de elektronen kunnen terug komen waar ze begonnen zijn.Voor de rest kan je stroom het beste vergelijken met een water stroom.
Je hoort wel een zeggen dat elektrische signalen zich met de snelheid van het licht voortplanten. Dat klopt maar daar moet je jezelf niet bij voorstellen dat de elektronen met de snelheid van het licht door de draden razen. Je moet het je meer zo voorstellen als de kraan bij je thuis. Als de de kraan opendraait komt er gelijk water uit. Dat betekend niet dat het water met een bloed-vaart uit de maas door de water zuivering naar je kraan toe vloeit (ander zou je wel even een kwartiertje moeten wachten tot er water uit komt). Nee de leiding zit vol met water en als je de kraan open draait komt het water er gelijk uit aan de andere kant (zeg maar de water zuivering ) stroomt het water er in met de zelfde vaart als het er bij de kraan uit komt. licht door de draden razen. Je moet het je meer zo voorstellen als de kraan bij je thuis. Als de de kraan opendraait komt er gelijk water uit. Dat betekend niet dat het water met een bloed-vaart uit de maas door de water zuivering naar je kraan toe vloeit (ander zou je wel even een kwartiertje moeten wachten tot er water uit komt). Nee de leiding zit vol met water en als je de kraan open draait komt het water er gelijk uit aan de andere kant (zeg maar de water zuivering ) stroomt het water er in met de zelfde vaart als het er bij de kraan uit komt.
Je krijgt zo'n beetje de situatie als figuur 3.
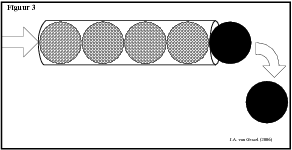 |
Stroom lijkt ook op water in de zin dat de hoeveelheid stroom (water) die naar een knooppunt toe vloeit er ook weer vandaan moet vloeien. (eerste wet van Kirchoff ). Dit mag een beetje onduidelijk zijn maar hopelijk verklaart figuur 4 alles.
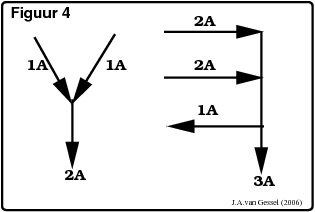 |
De eenheid van stroom is Ampère (A) en het symbool = I.
2.3.
Spanning is de kracht die op de elektronen staat ( in een water voorbeeld zou het waterdruk zijn) .
 |
In figuur 5 zie je ongeveer de situatie zoals ik hem mezelf altijd voorstel. In een vat met water met daaraan een pijp is de druk van het water de spanning en de hoeveelheid water die eruit stroomt de spanning.
De eenheid van spanning is Volt (V) en het symbool = U.
2.4.
Bij water is het logisch dat er bij gelijke druk uit een dikke pijp meer water stroomt dan uit een dunne. Dit wordt veroorzaakt door de stromings weerstand. Een dunne pijp heeft meer stromings weerstand dan een dikke. Het zelfde verschijnsel doet zich ook voor met elektriciteit. Sommige materialen hebben meer elektrische weerstand dan andere. Meneer Ohm heeft dat als eerste ontdekt en de wet van ohm opgesteld . Hij zei dat weerstand spanning gedeeld door stroom is.
| U |
| I |
De eenheid van weerstand Ohm (Ω ) en het symbool = R
Je hebt de wet van Ohm misschien anders geleerd namelijk.
Als je niet kan zien dat dat precies het zelfde is geef het dan even door dan leg ik dat een andere keer uit.
De wet van Ohm is een van de belangrijkste formules in elektro. Als je die kan onthouden kan je serie schakelingen parallel schakelingen en spanningsverliezen zonder problemen begrijpen . Maar daarover de volgende keer meer
3.
3.1.
Voordat we verder gaan met serie en parallel schakelingen nu eerst een klein beetje wiskunde. Wees niet bang ik zal het niet al te moeilijk maken.
Vergelijkingen ken je nog wel van school b.v.
AxB = C
Wat betekend dit nu precies ?. Er staat dat A maal B precies het zelfde is als C. Je kan het jezelf het beste zo voorstellen als je op een weegschaal aan de ene kant A maal B zet en aan de andere kant C dan is de weegschaal in evenwicht.
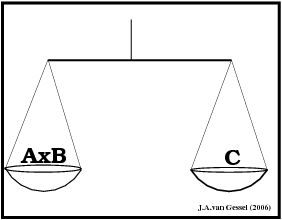 |
Zolang de linker en de rechter kant van de vergelijking in evenwicht zijn klopt de vergelijking.
In wiskunde wordt meestal het x teken (maal teken) weggelaten. In de rest van dit verhaal zal ik dat ook doen dus als je AB ziet staan betekent dat AxB.
Wat je in figuur 6 ziet staan is de vergelijking.
A B = C
Stel je nu de weegschaal voor als je er aan alle bij de kanten een C bij zou leggen zou de weegschaal nog steeds in evenwicht zijn dus klopt de vergelijking nog steeds.
A B + C = C + C ⇔ A B + C = 2 C is dus precies het zelfde als A B = C
Het zelfde geld natuurlijk met vermenigvuldigen. Als je alle bij de kanten van de weegschaal 2 keer zo zwaar maakt is hij nog steeds in evenwicht. dus:
2 A B = 2 C is ook het zelfde als A B = C.
Wat voor optellen en vermenigvuldigen telt telt natuurlijk ook voor aftrekken en delen.
Je zult nu ondertussen denken wat heb ik daar in gods naam aan. De vorige keer hebben we de formule U = I R behandelt. Die is heel makkelijk als je U wilt weten maar wat nu als je I wilt weten. Hoe maak je van de formule U = I R I = …………… ?
U = I R
deel nu alle bij de kanten door R
| U |
| R |
| I R |
| R |
je weet dat
| R |
| R |
| U |
| R |
| U |
| R |
dit lijk misschien wel wat omslachtig maar het werkt altijd en bij elke vergelijking dit in tegenstelling tot dat rare driehoekje wat je soms op school leert. Probeer maar een een leuk driehoekje te maken van
X1 =
|
||||
Voor de echte nerds op de volgende pagina heb ik een voorbeeld staan wat ik een tijdje geleden voor iemand heb gemaakt waarin ik alleen maar toepas wat hierboven staat om uit de vergelijking a x2 + b x + c = 0 een vergelijking x = ......... te maken. Maak je geen zorgen als je het niet helemaal begrijpt hij doet een hele andere opleiding als jij. Het kan je wel een indruk geven wat je met wat eenvoudige kennis allemaal kan uithalen.
3.2.
Oké laten we beginnen . Je hebt de formule en je wilt x isoleren
laten we aan het begin beginnen en eerst de a wegwerken door door a te delen
|
dat is het zelfde als
|
nu willen we het kwadraat van x wegwerken. Zoals je weet is ( a + b ) 2 = a 2 + 2 a b + b 2 we zouden hiervan gebruik kunnen maken om het kwadraat weg te werken. Als we voor a x invullen dan is 2 a b gelijk aan
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b2 |
| 4a2 |
| c |
| a |
| b2 |
| 4a2 |
nu kunnen we er een mooi volledig kwadraat van maken
| b |
| 2a |
| c |
| a |
| b2 |
| 4a2 |
nu kunnen we
| c |
| a |
| b |
| 2a |
| c |
| a |
| c |
| a |
| b2 |
| 4a2 |
| c |
| a |
| b |
| 2a |
| b2 |
| 4a2 |
| c |
| a |
nu kunnen we de breuk gelijknamig maken
| b |
| 2 a |
| b2 |
| 4a2 |
| 4ac |
| 4a2 |
| b |
| 2a |
| b2 - 4ac |
| 4a2 |
vervolgens kunnen we het kwadraat wegwerken
| b |
| 2a |
| b2 - 4ac |
| 4a2 |
zoals je weet heeft een kwadraat twee oplossingen een negatieve en een positieve dus
| b |
| 2a |
| b2 - 4ac |
| 4a2 |
| b |
| 2a |
| b2 - 4ac |
| 4a2 |
en
| b |
| 2a |
| sqrt2 (b2 - 4 a c) |
| 2a |
| b |
| 2 a |
| sqrt2 (b2 - 4a c) |
| 2a |
en eindelijk kunnen we x isoleren
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| sqrt2 (b2 - 4 a c) |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| sqrt2 (b2 - 4ac) |
| 2a |
dus
| - b + sqrt2 (b2 - 4a c) |
| 2a |
| - b - sqrt2 (b2 - 4a c) |
| 2a |
je ziet als je het principe weet is het eigenlijk betrekkelijk eenvoudig.
4.
Serie schakeling houdt in dat er twee dingen achter elkaar geschakeld worden. De uitgang van de ene komt in de ingang van de andere . In figuur 7 hieronder zie je een voorbeeld van in serie geschakelde weerstanden. Ze staan achter elkaar als olifantjes (de een houdt met z'n slurf de staart van de andere)
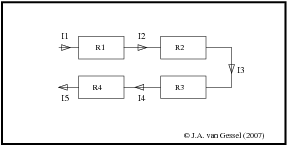 |
Een nog mooier voorbeeld van serieschakeling vind ik televisie series het einde van de ene aflevering is het begin van de andere.
4.1.
Zoals je je nog van de eerste les kan herinneren ( hoop ik ) is de stroom het aantal electronen wat per seconde door de leiding gaat ( het aantal pingpong balletjes ). Als er aan de ene kant bij R1 10 pingpong balletjes per seconde naar binnen gaan moeten er bij R4 10 pingpong balletjes per seconde uitgaan. Met andere woorden de stroom is overal gelijk.
Als het een waterleiding zou zijn zou er dus ongeacht het aantal vernauwingen in de leiding door ieder stukje van de leiding even veel water lopen ( zie fig 8 )
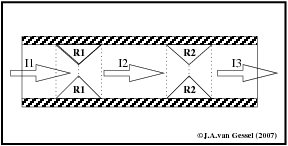 |
De hoeveelheid water die per seconde de pijp instroomt I1 is gelijk aan de hoeveelheid water die per seconde de pijp uitstroomt I3. Anders zou je ergens een lek hebben of ergens een extra water toevoer.
4.2.
Weerstand bij serieschakeling is ook heel makkelijk te begrijpen. Als de electronen door R1 gaan en een bepaalde weerstand ondervinden en ze komen door R2 en ze ondervinden nog eens zo'n weerstand dan hebben ze dus in totaal 2 x de weerstand ondervonden of beter gezegd.
Als je naar figuur 2 kijkt kan je je voorstellen dat de hoeveelheid weerstand die het water ondervind dat de pijp instroomt gelijk is aan de weerstand die het ondervindt bij vernauwing R1 plus de weerstand die hij ondervindt bij vernauwing R2.
4.3.
Spanning is misschien bij serieschakeling iets minder voor de hand liggend als stroom en weerstand. Ik zal het aan de hand van figuur 9 proberen duidelijk te maken. Je ziet daar dezelfde pijp als bij figuur 2 met de twee vernauwingen (weerstanden ) R1 en R2
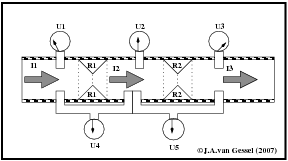 |
Als extra zitten er 5 drukmeters in de leiding U1 tm U5. De meters aan de bovenkant ( U1 tm U3) zijn gewone drukmeters. De meters aan de onderkant ( U4 en U5 ) zijn verschil druk meters en meten dus het drukverschil tussen in en uitgang. Wat gebeurt er nu? Het water stroomt de pijp binnen bij U1 de druk (spanning) is daar gewoon de druk van het leidingnet (zeg maar accu spanning ) . Als het water voorbij R1 stroomt verliest het een gedeelte van zijn druk. Als het water voorbij R2 stoomt verliest het de rest van zijn druk want de druk aan de uitgang ( gootsteen ) is 0. Als de weerstand van R1 en R2 even groot zijn heb je dus over alle twee het zelfde drukverlies.
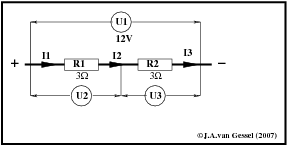 |
Laten we nu eens kijken hoe het bij een elektrische installaties zit. In figuur 10 zie je twee weerstanden R1 en R2. Voltmeter U1 meet de spanning over de twee weerstanden ( zeg maar accu spanning ) De voltmeters U2 en U3 meten het spanningsverlies over de weerstanden. I1 , I2 en I3 is de stroom door het systeem. Laten we nu even een rekenvoorbeeld nemen.
We weten dat de totale weerstand van R1 en R2 gelijk is aan R1+R2 dus.
| R totaal = R1 + R2 | ||
| R totaal = 3Ω + 3Ω | ||
| R totaal = 6Ω |
I1 = I2 = I3 De stroom wordt bepaald door de totale weerstand R totaal en de totale spanning (U1)
| U1 = I x R totaal | ||||||
| 12V = I x 6Ω | ||||||
|
||||||
| 2A = I | ||||||
| I = 2A |
Het spanningsverlies over R1 is dan.
| U2 = I x R1 | ||
| U2 = 2A x 3Ω | ||
| U2 = 6 V |
Je kan natuurlijk ook het zelfde verhaal ophangen voor R1 maar omdat alle waarden hetzelfde zijn zijn ook de antwoorden het zelfde. Je zal zien als je het met verschillende waarden voor R1 en R2 probeert dat (zolang R1 gelijk is aan R2) U2 en U3 altijd 6V zijn. Wat betreft spanningsverlies maakt de waarde van de weerstanden niet zoveel uit het gaat om de verhouding tussen de weerstanden. De grootste weerstand geeft het grootste spanningsverlies
Als je U2 en U3 bij elkaar optelt krijg je altijd de bron spanning.
Ik zal nog 1 rekenvoorbeeld geven met 2 verschillende weerstanden R1 is nu 2Ω en R2 is 4Ω
| R totaal = R1 + R2 | ||||
| Rtotaal = 2Ω + 4Ω | ||||
| Rtotaal = 6Ω | ||||
| U1 = I x Rtotaal | ||||
| 12V = I x 6Ω | ||||
|
||||
| I = 2A | ||||
| U2 = I x R1 | ||||
| U2 = 2A x 2Ω | ||||
| U2 = 4V | ||||
| U3 = I x R2 | ||||
| U3 = 2A x 4Ω | ||||
| U3 = 8V | ||||
Je ziet nu dat de stroom en de bron spanning gelijk is R2 is 2x zo groot als R1 en het spanningsverschil over R2 is dus ook 2 keer zo groot als over R1. Je ziet nu ook dat U2 + U3 gelijk is aan de bron spanning. Je had U3 dus ook als volgt kunnen uitrekenen.
| U bron = U2 + U3 | ||
| 12V = 4V + U3 | ||
| 12V - 4V = 4V + U3 - 4V | ||
| 8V = U3 |
Nu weet je dus hoe het zit met stroom spanning en weerstand in serieschakelingen. Je zal merken als je de simpele formule U = IxR kan onthouden je het grootste gedeelte al weet. Hierna zal ik parallel schakelingen behandelen.
5.
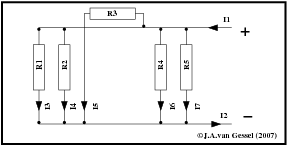
Bij parallel schakelingen worden dingen over elkaar aangesloten. Op de zelfde manier als ik mij serieschakeling voorstel als olifantjes stel ik mij parallel schakeling altijd voor als konijntjes ( die zitten meestal ook bovenop elkaar ). In figuur 11 zie je een tekening van een parallel schakeling. Let ook op weerstand R3 hij staat wat anders getekend dan de andere weerstanden maar is wel op de zelfde manier aangesloten. Afsluit weerstanden in canbus regelapparaten staan vaak zo bij ons in het schema getekend.
 |
5.1.
Laten we lekker makkelijk beginnen Alle weerstanden hebben 1 gemeenschappelijke pus en 1 gemeenschapplelijke min. Dus moet op alle weerstanden wel dezelfde spanning staan. In figuur 12 zie je een pijp die zich splitst in twee delen (parallel schakeling ). Het is dan logisch dat op de ingang ( U1 ) de wateleiding-druk (accu spanning ) staat en op de uitgang die in de gootsteen loopt 0 bar (de min) staat.
5.2.
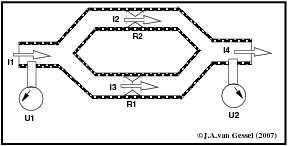 |
In figuur 12 zie je een bepaalde hoeveelheid water per tijdseenheid naar binnen lopen (I1). Die hoeveelheid verdeelt zich over de twee leidingen (I2 en I3) en komt tot slot weer als een stroom naar buiten (I4) je zou dus kunnen zeggen:
Hoeveel stroom er door ieder tak van de parallel schakeling heen loopt kan je uitrekenen met de aloude formule U = IxR . Laten we nu eens uitgaan van figuur 12. Stel R1 = 6Ω R2 = 6Ω en U = 12V. (U1=12V U2=0V dus U=12V).
Om I2 uit te rekenen kunnen we dus zeggen
| U = I2 xR2 | ||||
| 12V = I2x6Ω | ||||
|
||||
| 2A = I2 |
Omdat R1 en R2 gelijk zijn is de stroom door R1 ook 2A (I3=2A)
| Itotaal = I2 + I3 | ||
| Itotaal = 2A + 2A | ||
| Itotaal = 4A |
5.3.
Over weerstand bij parallel schakeling wordt nog al eens moeilijk gedaan om dat de formule ervoor zorgt dat je met breuken moet werken. Dus zal ik in dit geval eerst een uitleggen wat er gebeurt voordat we de formule erbij pakken.
Bij het voorbeeld wat we net uitgerekend hebben zien we dat er door R1 2A loopt .Als we daar een weerstand parallel aan schakelen loop daar ook stroom door in het voorbeeld ook 2A. Zouden we R1+R2 moeten vervangen door 1 weerstand dan zou er door die ene weerstand dus 2A+2A=4A moeten lopen. Gelukkig hebben we de wet van Ohm om die weerstand uit te rekenen.
| U = Itotaal x Rtotaal | ||||
| 12V = 4A x Rtotaal | ||||
|
||||
| 3Ω = Rtotaal |
De totale weerstand wordt dus kleiner dan de weerstanden afzonderlijk zijn. Als je twee weerstanden van 6Ω parallel geschakeld is de totale weerstand 3Ω. Het is belangrijk om te weten dat de totale weerstand altijd kleiner is als de kleinste weerstand. Immers door de andere weerstanden loopt ook stroom. Natuurlijk is er ook een formule om de vervangings-weerstand uit te rekenen. En die is:
| 1 |
| Rtotaal |
| 1 |
| R1 |
| 1 |
| R2 |
| 1 |
| Rx |
Als we nogmaals het bovenstaande voorbeeld nemen krijgen we dus
|
||||||||
|
||||||||
|
||||||||
Rtotaal =
|
||||||||
| Rtotaal = 3Ω |
Ik neem aan dat de meeste van jullie handig genoeg zijn met jullie rekenmachines om dit zelf uit te rekenen. De meeste moderne rekenmachines kunnen tegenwoordig rechtstreeks in breuken werken. Mocht er toch nog behoefte zijn in een uitleg van het rekenen met breuken of hoe je dit moet doen met je rekenmachine laat het me even weten dan kan ik daar ook nog wat aandacht aan besteden.
De volgende keer gaan we met al die teoretische kennis iets praktisch doen.
6.
6.1.
Tijdens de vorige werkplaats vergadering was er nog al wat discussie over het beperken van het internet gebruik. Naast de bandbreedte die het opslurpt is er ook nog een veiligheidsaspect. Ik ben wel samen met jullie van mening dat de meeste bandbreedte niet door de werkplaats wordt gebuikt en dat wij over het algemeen de computers op het werk wel redelijk veilig gebruiken.
Maar het viel me toen wel op dat de meeste van jullie niet echt een idee hebben wat er fout kan gaan op het gebied van veiligheid. Het ligt niet in mijn bedoeling iedereen bang te maken om internet te gebruiken of om een heel verhaal te houden over virus scanners of firewalls maar meer om iedereen logisch na te laten denken als hij op het internet bezig is.
6.2.
Uit het oogpunt van de gebruiker is het makkelijk . Je toetst een adres in en je krijg de pagina op het scherm. In feite gebuurt er veel meer. Ik zal wat dingen er uit lichten.
Ten eerste de naam die je intoetst wordt naar een DNS server verzonden . Dat is een computer die de naam omzet in een nummer. Alle computers op het internet hebben een nummer . Een DNS server is dus een grote lijst met wel nummer er bij welke naam hoort.
Dat nummer wordt teruggestuurd naar jou computer en vervolgens geeft jou computer het commando HTGET wat naar de computer met dat nummer wordt gestuurd.
Die computer reageert dan door een HTML pagina naar jou computer terug te sturen. Die jou computer dus download. Het argument ik kijk alleen maar wat rond en download niets gaat dus niet op. HTML is alleen maar tekst. Dit is een stukje van mijn eigen web pagina.
<h2><a id="Copyright"> Copyrights </a> </h2>
</p>Alles wat je op deze pagina’s vindt kan je naar eigen goeddunken gebruiken. Doe er mee wat je wild. Maar externe links verwijzen naar andere sites en die hebben hele andere opvattingen over copyrights. Dus controleer eerst voordat je hun gegevens gebruikt.</p>
Als je alles wat tussen haakjes ”<” en ”>” en alles wat tussen ”&” en ”;” weglaat heb je gewoon leesbare tekst. De computer gebuikt alles wat tussen haakjes staat voor de opmaak van de tekst b.v. in het voorbeeld hierboven ”<h2>” betekend dat de tekst iets groter en op het midden van de pagina wordt getoond. Hiervoor is HTML gemaakt en ook behoorlijk veilig.
6.3.
Het grote probleem is dat mensen geen tekst op het internet bekijken maar plaatjes geluid, animaties, filmpjes, spelletjes, enz. enz. . Met als gevolg dat internet-browsers steeds worden aan gepast om daarmee om te gaan en dus steeds groter worden ( internet explorer 2 past op 1 floppy van 1,4Mb ). Of er worden aparte hulp programma's gemaakt om met die gegevens om te gaan denk maar aan realplayer, acrobat viewer, flash player, media player enz. enz. .
Hoe groter een programma is hoe groter de kans op fouten. Als er steeds meer programma's zijn wort de kans nog groter omdat er in de interactie tussen de programma's's ook veel fout kan gaan. Meestal zijn die fouten alleen maar lastig. Soms echter zijn de fouten van dien aard dat iemand van buitenaf controle over jou computer kan krijgen. Als zo een fout bekend is doet hij zich ook razend snel de rondte (dat is het nadeel van internet) en omdat de programma's zo groot zijn geworden kan het soms wel maanden duren eer dat ze hersteld zijn.
De andere kant van het verhaal is natuurlijk dat wij ook vaak willens en wetens de controle over onze computer aan een ander geven.
” Om deze pagina te bekijken heeft u de xxx plug-in nodig klik op ok om te installeren”
Op die manier geef je dus een ander toestemming om een programma te installeren op jou computer.
6.4.
Het meest logische ( zou je denken ) is natuurlijk inlog gegevens van je bank, pas-nummers, email adressen, inlog gegevens van je web site, credit kaart nummer e.d. . En het is waar die worden ook heel vaak misbruikt. Maar tegenwoordig is het vaak voldoende dat ze als het nodig is controle over je computer hebben.
Het kan zo zijn dat er tijden lang niets mee gedaan wordt door de mensen die jou computer onder controle hebben. Maar ze hebben b.v. 10.000 computers die ze kunnen inzetten als het nodig is ( een bot-net ). Om zelf buiten schot te blijven worden die meestal aan derden verhuurd. Door ze op commando allemaal gelijk iets op te laten vragen bij een web site is de web site tijdelijk niet bereikbaar voor anderen (het gaat in werkelijkheid iets anders). De criminelen nemen dan contact op met het bedrijf en eisen geld.
Bij Volkswagen, I.B.M. of de Nasa zal dit weinig effect hebben want die hebben kennis geld en mankracht genoeg om te achterhalen wat er gebeurt en de politie in te schakelen. Maar de internet-pizza bakker die al een aantal dagen geen inkomsten heeft omdat zij web site tussen 8 en 10 uur plat ligt zal al gouw in de verleiding komen om maar te betalen.
Nu voor het verspreiden van spam steeds vaker straffen worden uitgedeeld is zo'n bot-net ideaal. De spam wordt immers verspreidt door vele verschillende computers en het is lastig om te achterhalen wie er achter zit.
Helaas levert het verspreiden van kinder-porno ook nog steeds grof geld op. In Nederland is het hebben , verspreiden of zelfs bekijken van kinder porno strafbaar. Als er dus op jou computer bestanden staan die er door anderen opgezet zijn ben je dus in principe als strafbaar. Als jij kan bewijzen dat het buiten jou medeweten is gebeurd wil een rechter het nog wel door de vingers zien ( maar ja bewijs dat maar eens ).
6.5.
Daar kan ik kort in zijn NADENKEN !!!!.
Naast het regelmatig uitvoeren van updates en een virus scanner e.d. is het nadenken wat je doet het belangrijkst (misschien wel belangrijker ).
Ga er niet van uit dat je veilig bent omdat je regelmatig updates uitvoert. Je kan namelijk pas een probleem verhelpen als het probleem bekend is (dan kan het al te laat zijn )
Kijk eens op de onderste regel van je web browser voor je op een link klikt (daar staat waar de link werkelijk naartoe verwijst ) Als je naar b.v. de site van fijenoord wil en op de onderste regel staat http://www.gevaarlijke-botnetbeheerder.ru dan klopt er iets niet.
Kijk uit met software waar je de herkomst niet van weet ( file sharing e.d. ) je weet immers niet wat ze er aan veranderd hebben om het nog onveiliger te maken.
Installeer niet blindelings dingen vanaf het internet. Heb je die plug in wel echt nodig??. Kan ik de site vertrouwen waar hij vandaan komt?
Kijk uit met veel bezochte sites Youtube ,Hives e.d. dat is namelijk de ideale plek op je speciaal geprepareerde filmpjes, web pagina's e.d. te verspreiden.
Wees voorzichtig met het openen van word exell powerpoint kortom alles wat een apart programma opstart.
6.6.
Alles wat ik hierboven vertel geld ook voor het normale computer gebruik. Dus kijk uit met het openen van mail, Office documenten e.d. . Soms is het bekijken van een plaatje of document al genoeg. Zoals je moeder al zei neem geen snoepjes aan van vreemden.
Zoals jullie weten ben ik geen groot fan van Microsoft. De veiligheid van Windows ligt nog al eens onder vuur. Het is nu tegenwoordig zo dat 90% van de mensen windows gebruikt en ongeveer 80% van de mensen internet explorer. Daarom zijn de meeste aanvallen daarop gericht. Zou 90% van de mensen Linux ,FreeBSD ,Qnx ,eComstation ,Zeta of wat dan ook gebruiken zouden de aanvallen daarop gericht zijn. Het is natuurlijk wel zo dat als er meer diversiteit is de kans op grootscheepse aanvallen kleiner wordt (dus probeer eens iets anders en maak het internet veiliger )
Ik weet zeker dat ik door dit verhaal niemands internet gedrag heb veranderd. Maar hou het in je achterhoofd en bedenk dat internet en computers in het algemeen gewoon leuk zijn.
7.
Deze lessen zijn gemaakt op een pentium III 800 MHz computer met 512MB aan Geheugen. Het besturingssysteem is FreeBSD 6.2-stable (zie http://www.freebsd.org) . Op zie computer staat Xorg (zie http://www.x.org) geïnstalleerd. De windowmanager is Matchbox (zie http://matchbox-project.org/)
De teksten zijn gemaakt met Texmacs (zie http://www.texmacs.org) en de plaatjes met xfig (zie http://www.xfig.org) . De reden dat ik Texmacs gebruik is omdat alleen al de formule editor de moeite van het installeren waard is. Texmacs is behoorlijk groot omdat het op Tex (zie http://www.ntg.nl) gebaseerd is. Maar dat houd ook in dat je erg goede export naar pdf en postscript hebt. Ik exporteer meestal naar pdf omdat dat op alle besturings systemen waar ik mee te maken heb goed te printen is zonder verlies aan opmaak.
Zoals je ziet is alle gebruikte software opensource ( de broncode is beschikbaar ) en in dit geval ook nog eens gratis. Dat houdt dus in dat je geen licentie kosten of aanschafkosten voor de software hebt en dat je ook niets hoeft te kopen (als je tenminste een flat-rate internet verbinding hebt). Je hoeft dus ook geen illegale downloads op je computer te installeren (met alle risico's van dien )
Ik heb zelf alles inclusief het besturingssysteem van broncode gecompileerd (hoeft niet hoor) voor een pentium III en aangepast op deze computer (wat redelijk makkelijk gaat met FreeBSD).Hierdoor heb je een kleine snelheids winst (maar alle beetjes zijn meegenomen )
Zoals je ziet heb je niet de duurste beste of nieuwste spullen te kopen om een redelijk resultaat te krijgen.
8.
8.1.
Ik vindt het altijd leuk om wat ludiek voorbeelden te geven. Als ik terugdenk aan de lessen die ik heb gehad zijn dat de lessen die het beste blijven hangen. Het houdt ook een beetje de spanning er in ( waar zal hij nu weer mee komen ... ).
Dit zijn de dingetjes die ik gemaakt heb. Het is niet mijn bedoeling om een complete handleiding te maken maar misschien inspireren ze. De les materialen zijn per les en hoofdstuk verdeeld.
8.2.
8.2.1.
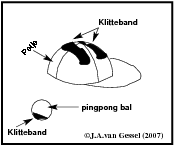
Om het atoom inzichtelijker te maken heb ik zes ping-pong ballen genomen, 2 (de protonen) gemerkt met een plus (met viltstift ) de 2 neutronen ongemerkt gelaten en de 2 electronen gemerkt met een min. De protonen en de neutronen heb ik beplakt met klittenband . Ook heb ik een petje beplakt met klittenband. (zie figuur 13) .Als je het petje beplakt met de protonen en de neutronen heb je een atoomkern. Als je dan de een electron in iedere hand neemt heb je een atoom .
 |
8.2.2.
Als je met het zelfde petje als bij figuur 13 je iemand een ping-pong bal laat aangeven kan je laten zien dat je dat je om die pingpong-bal aan te nemen er eentje moet doorgeven aan de gene naast je en heb je een leuke illustratie van een electronen stroom.
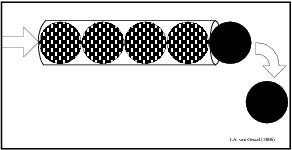 |
Om de voortplantings snelheid van electrische signalen te demonstreren heb ik een keukenrol genomen ( in mijn geval paste daar precies de ping-pong balletjes in ) . Door hem te vullen met pingpong ballen en er aan 1 kant 1 bij te doen komt er aan de andere kant 1 uit. Het signaal heeft zich over de lengte van de keukenrol verplaats en de afstand die die electron aflegt is de grootte van 1 electron. Zie figuur 14. (opm. plaatje is rechtstreeks overgenomen uit de tekst )
8.2.3.
Door twee gelijke stukjes pvc-pijp te nemen en eentje gedeeltelijk af te sluiten kan je weerstand illustreren. Het gedeeltelijk afsluiten heb ik in mijn geval gedaan door eerst het pijpje te vullen met gatenvuller en er toen een klein boorgat in te boren.
Als je de ballonnen opblaast heb je door de grootte van de ballon een indicatie van de druk ( spanning ).
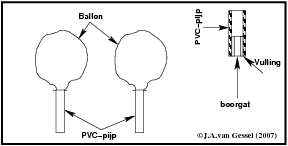 |
Als je de ballonnen door de pvc-pijpjes laat leeglopen is de snelheid van de lucht die er doorheen stroomt een indicatie van de stroom (kan je zien aan hoe snel de ballon leeg is ). De weerstand van het gedeeltelijk afgesloten pijpje is gorter en bij de zelfde druk stroomt de lucht er minder snel doorheen ( U = I x R )
8.3.
Om vergelijkingen wat te verduidelijken heb ik een weegschaal (balans) gemaakt van een pvc-pijpje (zie afbeelding)
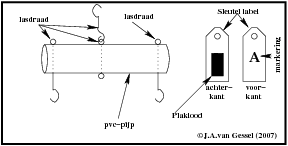 |
Door er drie gaatjes doorheen te boren en er met lasdraad 2 haakjes en een ophang beugel aan te maken heb je en balans die niet al te gevoelig is (ander moet je zo nauwkeurig werken ). Door wat sleutel labels te nemen en die aan 1 kant te beplakken met plaklood (plakzink) . En aan de andere kant met een A, B of C te markeren.
A=30gr
B=20gr
C=10gr
kan je dus door aan de ene kant een label A te hangen en aan de andere kant een B en een C te hangen de vergelijking A=B+C vormen. Door er aan allebei de kanten er nog een zelfde label bij te hangen (bv een C) kan je dus aantonen dat je er aan bijde kanten hetzelfde bij mag optellen. Door ze er weer af te halen kan je laten zien dat het zelfde geld voor aftrekken. Vermenigvuldigen (bv met 2) kan je laten zien door aan de ene kan 2 x A op te hangen en aan de andere kant 2 x B en 2 x C en om delen te laten zien kan je er weer 1 A, B en C afhalen.
Doordat B 2xC = kan je ook nog substitutie van B door 2xC laten zien
totaal hen je dus nodig
2x A (30gr)
2x B (20gr)
3x C (10gr)
9.
9.1.
Deze trainingen zijn mede tot stand gekomen door een aantal mensen die ik graag wil noemen.
De computer waarop ik dit maak is de oude computer van de kunstenares Sija Vermaat ( zie http://www.kunstkringvoorne.nl/vermaat_sija.htm )
De server ruimte waar deze website op draait is gedoneert door Tasman Webdesign ( http://www.tasman-webdesign.com ) die ook de domijnnaam registratie heeft verzorgd.
Het beeldscherm waar ik dit op maak is een oud beeldscherm van M. de Koning b.v. waar ik werk ( zie http://www.mdekoning.nl )
9.2.
Om de kosten binnen de perken te houden en uit principe maak ik alles op opensource software die gratis en vrij is. ( zie ook hoofdstuk Gebruikt Materiaal )
9.3.
Dit zijn de kosten die ik heb gemaakt om de computer geschikt te maken voor het maken van de lessen. De usb-stick is om bestanden over te brengen naar het werk (voordat de website gedoneert werd) De cd brander is voor backups (iets wat je echt nodig hebt op een oude computer )
| computer | 0.00 |
| monitor | 0.00 |
| website | 0.00 |
| muis | 8.00 |
| usb-stick | 11.20 |
| cd-brander (2e hands) | 10.00 |
| 256 MB geheugen | 24.00 |
| Totaal | 53.20 |
9.4.
Dit zijn de kosten die per les gemaakt zijn. Ik heb ook een uurtarief 8 eu per uur opgeschreven ( helaas niet gekregen .... ) mat mij aller-sinds redelijk lijkt.
9.4.1.
| tijd 10 uur | 80.00 |
| pingpong balletjes | 1.99 |
| rol klittenband | 3.00 |
| ballonnen | 0.00 |
| petje | 0.00 |
| Totaal | 84.99 |
9.4.2.
| tijd 4 uur | 32.00 |
| pvc pijp | 2.00 |
| 3 strips plaklood | 0.00 |
| Totaal | 34.00 |
9.4.3.
| tijd 8 uur | 64.00 |
| Totaal | 64.00 |
9.4.4.
| tijd 8 uur | 64.00 |
| Totaal | 64.00 |
9.4.5.
9.5.
|
||||||||||||||||||||||||||||||
|